Back to developing algotihm for wet stagnant bed thermal conductivity. Yet found well advised correlation called Zehner-Bauer-Schlunder model.
http://hedhme.com/index/?link_id=12165&article_id=200

This is so massive - allmost 30sets of equations joining moisture content, porsity, free air voids remaining both in macropores- what is the general structure of the solid, but also in micropores- those understood as air voids in the bed itself- connected with bulk density. Very logically build one, I mean as a logiacal way of approximating in the all directions effects of condutivity given by each of the components additively, even including diffusion effect in pores ;)
However, practically the possible standard deviation is +-30%
What the hell??

I know it is solid- but Are there any better models as this follows on 90ties?

Now from my knowledge and experience I know that boundary conditions are moisture content of 0% and 100%, temperatures for both air and material ranging from even -30 to 150 deg Celsius.
Yet remains the necessity of finding internal temperature between gas core and core of the solid to precisly give all the details to declare the thermal conductivity by diffusion.
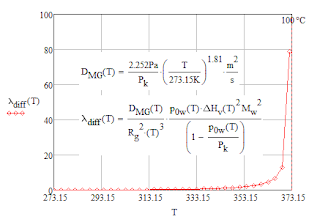
Here's a plot of this value with temperature under the whole range of the dryers work.
it rises even to 80Watts/m*K!

Someone could think it is maybe not important, but the temerature during drying rises and this is an exponential function of temperature hidden in the exponential behavior of vapor pressure. First equation is an approximation of diffision coefficient of saturated pressure. The next one is Schlunder and Tsotsats'  derived model available here
http://www.sciencedirect.com/science/article/pii/0255270186800216
This is very important so to precisly give the temperature because a mistake of 10 degrees can radically change final value of thermal conductivty of the bed!
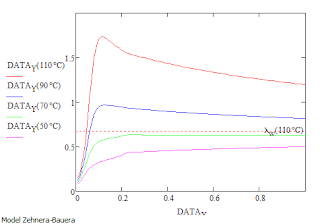
Heres's a simplified plot of the model not including the model of the internal temperature. Here belon the interal temperature if needed in Schulners diffusive model and other is simplified to the average of gas and solid temperature. The plot represents the wet bed thermal conductivity vs moisture content of the solid. This may be a cause for step temperature rise at the end of drying.
Gas temperature here is very low 10deg. The family of curves is marked with colours representing different material temperature

Especailly this diffusion process takes place from the middle of the solid towards the surface. This is imporant to take the the average of both temperatures or use even better estimations.
So the surface temperature is needed?
I've done this setting the heat balance equations on the surface and it is:
Latent heat of vaporized water- Heat transfered to air by convection= Heat transfered by sum of conduction, convection and condution of dryers wall as well as convection on the other side of the wall.
It is possible to easy calculate but the numerical calculations must be done as some models need to use vapour pressure- and this is an exponential function, unfortunatelly.
Some all in all the calculation for thermal conduction of stagnant packed bed lasts a about 2 second, but if u want to integated over whole range precisly the system would be stiff and the grid density is very important as well. So is really prolong the calculations.

Is it worth to recorelate thermal conduction as a function of temperature before each step of the integrator?


#stagnant_packed_beds