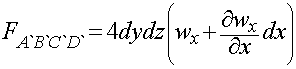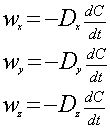Równanie Ficka- Prawa Dyfuzji

Postanowiłem wyprowadzić śladami pana Adolfa Ficka jego prawa dyfuzji, aby lepiej zrozumieć ten temat.
Natrafiłem na pewien artykuł z książki, który nieco przerobiłem i uprościłem na "swój język". Oto cały logiczny ciąg.

Mieszaninę płynów podczas zjawiska dyfuzji, jak zresztą każdy płyn można opisać posługując się tzw. sześcianem różniczkowym płynu. Jest to pojęcie dość abstrakcyjne, jednak, takowa mikroskopowa analiza pozwala na wyjaśnienie makroskopowych zależności. Jeżeli bowem układ jest różniczkowy to zmiany, posługując się językiem potocznym, są na tyle małe, że praktycznie nie zaburzają stabilności tego układu i można rozpocząć rozważania nad nim, bo warunki są pseudoustalone. Innymi słowy, przy tak mikrospokopwej analizie nic sie nie dzieje... w makroświecie jednak zachodza poważne zmiany.
Jednak do rzeczy...

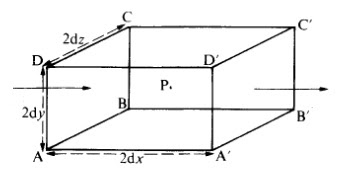
... Modelowy sześcian rożniczkowy składa się z trzech ścian o wymiarach geometrycznych odpowiednio:
- dla ścian pionowych: 2dy
- dla ścian poziomych (w płaszczyśnie ekranu): 2dy
- dla ścian ukośnych (wgłąb ekranu): 2dz
Sześcian ten ma wierzchołki odpowiednio oznaczone ABCD oraz A`B`C`D`. Jeżeli w sześcianie tym zachodzi dyfuzja nalezy rozpatrzeć wszystkie, siły dyfuzyjne działające na każdą ze ścian sześcianu, a w zasadzie wszystkie zewnętrzne i wewnętrzne zjawiska zmieniające skład w układzie.
Rozpatrując o zmiany w osi x, możemy zapisać strumień dyfuzyjny masy dopływający do ściany ABCD:

Przez w, rozumiemy prędkość masową dyfuzji w kmol/m^2*s. Prędkość ta jest uniwersalna ponieważ jest niezależna od powierzchni przepływu substancji dyfundujących oraz czasu dyfuzji. Ponieważ posługujemy się różniczkową prędkością masową, jej zmiana w czasie praktycznie nie następuje. Prędkość ta wymnożona przez powierzchnie dyfuzyjną będzie miała wymiar strumienia molowego, a w zasadzie molowego strumienia dyfuzji.
Z drugiej strony sześcianu dyfuzyjny strumień molowy wygląda następująco:

Przechodzi on przez płaszczyznę A`B`C`D`.
Jak widać strumień dyfuzyjny przechodząc przez sześcian płynu, zostawia "nieco" masy w jego środku (Właśnie to nazywamy dyfuzją). Można zatem zapisać prawo bilansu i zobaczyć "ile" strumienia zostało w środku. Wiadomo, że różnice między dopływem, a odpływem stanowi akumulacja:

Występowanie różniczki niezupełnej wskazuje uważenemu czytelnikowi, że jest ona tylko składową na pewnej płaszczyźnie. Logicznym jest oczywiście, że występują jeszcze dwa strumienie dyfuzyjne działajace na każdą płaszczyznę. Sumarycznie dostajemy trzy równania na każdą z płaszczyzn:

W tym momencie, zaczyna się zupełnie nowe podejście do rozważań i wprowadzamy dodstkową wiadomość która spaja wszytko w jedną całość. Mianowicie, należy zauważyć że w omawianym sześcianie skutkiem zmiany strumienia dyfuzyjnego na długości jest zmiana stężenia w czasie. Poza tymi zmianami na czterech elementach czasoprzestrzeni nic więcej się nie zmiania. Zatem bilansując zmiany w układzie można zapisać

Wynika z tego, że pochodna stężenia po czasie jest proporsjonalna do ujemnego gradientu prędkości masowych po wszystkich wymiarach przestrzennych.
Założenie teorii Ficka opiera sie na proporcjonalności prędkości masowej w każdej z płaszczyzn do ujemnego gradientu stężenia po czasie.

Po uwzględnioniu tej zależności w poprzednim wzorze, otrzymujemy:

Jest to najbardziej ogólna postać prawa Ficka. Uwzględnia ona zmienność strumieni dyfuzyjnych, jak również zmienność stałej dyfuzji (stała dyfuzji może być funkcją x,y,z oraz stężenia), a także dyfuzję we wszystkich płaszczyznach. Kolejne przekształcenia doprowadzają nas do postaci skróconych i pewnych szczególnych przypadków:
Następująca postać, zakładająca stałą dyfuzyjność z czasem i wymiarami geometrycznymi. W praktyce oznacza to homogeniczność składu mieszaniny dyfuzyjnej.

Kolejne uproszczenie polega na założeniu, że dyfuzja zachodzi tylko w jednej płaszczyźnie. Prowadzi to do wzoru, który jest powszechnie znany jako drugie prawo dyfuzji Ficka:

Jeżeli natomiast założyć, że prędkość masowa dyfuzji (strumień dyfuzyjny) jest stały w czasie, czyli że rozkład stężenia na drodze dyfuzji jest niezmienny, w trakcie trwania dyfuzji, otrzymujemy:

Co po scałkowaniu nazywane potocznie jest pierwszym prawem Ficka.

Problem podstawiania w Mathcadzie/ The matter of substitution in Mathcad

Najpierw definiujemy daną zmienną, a następnie poniżej wybieramy explicit dla tej tej samej zdefiniowanej zmiennej. Składnia explicit'a jest następująca: najpierw piszemy symbol zdefiniowanej zmiennej, następnie wybieramy z palety symbolics słowo kluczowe explicit, dajemy przecinek, a po przecinku wszystkie zmienne pod które ma nastąpić podstawienie. Schemat jest następujący. Jeżeli pod zmienną są inne zmienne wcześniej definiowane to mathcad bedzie podstawiał, tylko te zmienne które są zdefiniowane po explicit. Działa to w ten sposób, że pod Prandtla zdefiniowanego w ty arkuszu po słowie explicit trzeba koniecznie ponowić symbol prandta. Jeżeli bedzie to jedyny keyword po explicit mathcad zwroci definicje prandtla, jeżeli dalej bedziemy wpisywać zmienne z samej definicji Prandtla to Mathcad wyświetli ich definicje. Poprzez słowo definicja, mam na mysli zarówno wartość liczbową jak i sam wzór.

Jak widać na pierwszym screenie wartość współczynnika przewodzenia ciepła nie została podstawiona właściwie. Zdarza się to dość często, mimo iż wcześniej ją obliczaliśmy. Moje rozwiązanie problemu przedstawia rysunek numer 2. Ponieważ boczne strony arkusza nie są przewidziane do druku wykonuje tam tak zwaną redefinicję zmiennych. Redefinicja współczynnika przewodzenia ciepła musi znajdować się przed samą definicją Prandtla, aby explicit mógł zrozumieć, że ma podstawić wartość współczynnika a nie wzór. Stąd, piszemy symbol współczynnika przewodzenia ciepla, podstaw...znów symbol współczynnika przewodzenia ciepła i KONIECZNIE "zwróć wartość". Całość jak już powiedziałem musi się znajdować przed definicją Prandtla. Jeżeli więcej niż jedna zmienna jest niewłaściwie podstawiana trzeba zrobić zabieg jej redefinicji ponownie. Przyczyn różnego podstawiania możę być wiele i wynikają one z wcześniejszych linijek arkusza. Ogólnie jest tak, że w forumule explicit mathcad do podstawienia pobiera ostatnią formułę definicji. Jeżeli definicja nie będzie zawierała na końcu zwrócenia wyniku mathcad za każdym razem będzie pobierał całą formułę. Jeżeli będzie wynik to wstawia go od razu.

Po kliknięciu prawym klaiwszem myszy na słowo kluczowe explicit otwiera nam się menu rozwijane, w którym możemy wybrac opcje przedstawiania całego wyrażenia przez mathcada. Do wyboru mamy Hide Keyword, czyli ukrywanie słowa kluczowego explicit i wszystkich zmiennych do których się podstawia (tzw. modifiers). Można także ukryć lewą stonę przed strzałką czyli w tym przypadku definicję Prandtla wybierając opcje Hide left-hand side. A w opcja "view evaluation as" dokonujemy wyboru wyświetlania znaku wskazującego wynik podstawienia: strzałka, znak równości lub opcja standardowa tak jak zdefiniowano w opcjach arkusza (tak jest u mnie). Z tego co mi wiadomo nie da się przedstawić jednostek w postaci ułamków zwykłych lub pominąć ich podstawianie. Można oczywiście obliczenia prowadzić bez jednostek mając na uwadze operacji na jednostkach podstawowych SI. PTC nie wpadło chyba jeszcze na pomysł, że można byłoby osobno traktować jednostki i osobno wartości liczbowe w arkuszu, wtedy dużo rzeczy było by prostszych.